این مثال نشان میدهد که چگونه میتوان از بلوکهای Simulink® و توابع کمکی ارائهشده توسط Robust Control Toolbox™ برای مشخص کردن و تحلیل سیستمهای نامشخص در Simulink استفاده کرد و چگونه میتوان از این ابزارها برای انجام شبیهسازیهای مونت کارلو بر روی سیستمهای نامشخص بهره برد. مقدمه مدل Simulink به نام usim_model شامل یک گیاه نامشخص در بازخورد با یک حسگر است:
openExample('robust/usim_demo')
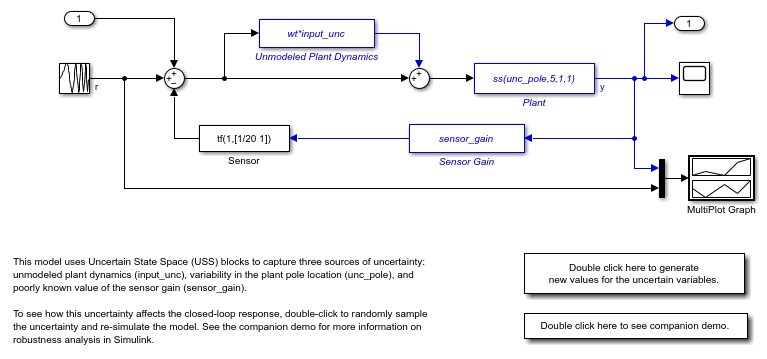
این گیاه یک مدل اولین مرتبه است که دارای دو منبع عدمقطعیت میباشد: قطب واقعی که موقعیت آن بین -10 و -4 متغیر است. دینامیکهای مدلنشده که به میزان 25% عدمقطعیت نسبی در فرکانس پایین و تا 100% عدمقطعیت در 130 رادیان بر ثانیه میرسند. مسیر بازخورد دارای یک سنسور ارزان است که با یک فیلتر اولین مرتبه در 20 رادیان بر ثانیه مدلسازی شده و دارای تقویت نامشخصی است که بین 0.1 و 2 متغیر است. برای مشخص کردن این متغیرهای نامشخص، تایپ کنید.
% First-order plant model
unc_pole = ureal('unc_pole',-5,'Range',[-10 -4]); plant = ss(unc_pole,5,1,1);
% Unmodeled plant dynamics
input_unc = ultidyn('input_unc',[1 1]); wt = makeweight(0.25,130,2.5);
% Sensor gain
sensor_gain = ureal('sensor_gain',1,'Range',[0.1 2]);
بلوکهای سیمولینک برای مدلسازی و تحلیل عدمقطعیت
کتابخانه RCTblocks شامل بلوکهایی برای مدلسازی و تحلیل اثرات عدمقطعیت در سیمولینک است. برای باز کردن کتابخانه، تایپ کنید
open('RCTblocks')

بلوک فضای حالت نامشخص به شما این امکان را میدهد که سیستمهای خطی نامشخص (اشیاء USS) را مشخص کنید. مدل usim شامل سه بلوک از این نوع است که با رنگ آبی هایلایت شدهاند. دیالوگ بلوک "پلان" در زیر نمایش داده میشود.

در این کادر گفتوگو، پارامتر "متغیر سیستم نامشخص" مدل سیستم نامشخص (مدل مرتبه اول با قطب نامشخص unc_pole) را مشخص میکند. پارامتر "مقدار عدم قطعیت" مقادیر متغیرهای نامشخص بلوک را مشخص میکند (در این مورد unc_pole). uval یک ساختار است که نامها و مقادیر فیلدهای آن، نامها و مقادیر متغیرهای نامشخصی هستند که برای شبیهسازی استفاده میشوند. میتوانید uval را تنظیم کنید تا از مقادیر نامی برای متغیرهای نامشخص استفاده کنید یا uval را تغییر دهید تا تحلیل کنید چگونه عدم قطعیت بر پاسخهای مدل تأثیر میگذارد. بلوک گراف MultiPlot یک روش مناسب برای تجسم پراکندگی پاسخها به هنگام تغییر عدم قطعیت است. این بلوک نتایج شبیهسازی بهدستآمده برای هر مقدار عدم قطعیت را روی هم قرار میدهد.
شبیهسازی مونت کارلو از سیستمهای نامشخص
برای کنترل آسان مقدار عدم قطعیت استفادهشده برای شبیهسازی، usim_model از همان "مقدار عدم قطعیت" uval در هر سه بلوک فضای حالت نامشخص استفاده میکند. تنظیم uval به [] پاسخ حلقه بسته را برای مقادیر نامی unc_pole، input_unc و sensor_gain شبیهسازی میکند:
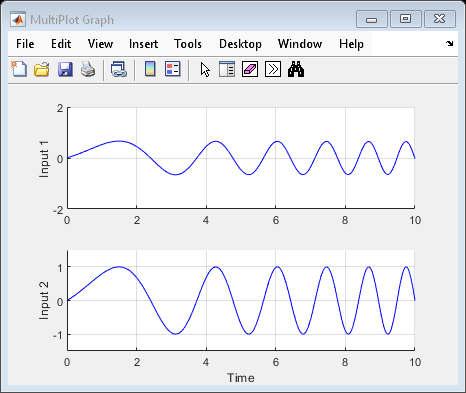
uval = [ ]; % use nominal value of uncertain variables
sim('usim_model',10); % simulate response
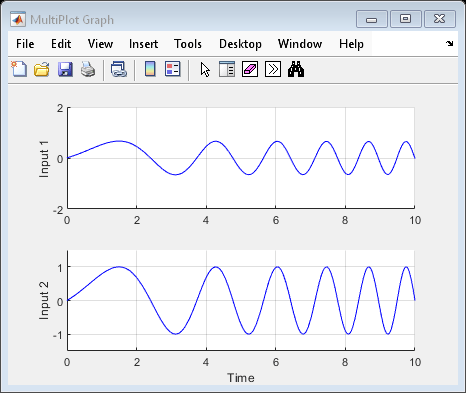
برای تحلیل اینکه چگونه عدم قطعیت بر پاسخهای مدل تأثیر میگذارد، میتوانید از دستورات ufind و usample برای تولید مقادیر تصادفی از unc_pole، input_unc و sensor_gain استفاده کنید. ابتدا از ufind برای پیدا کردن بلوکهای فضای حالت نامشخص در usim_model استفاده کنید و فهرستی از تمام متغیرهای نامشخص در این بلوکها تهیه کنید:
[uvars,pathinfo] = ufind('usim_model'); uvars
% uncertain variables
= uvars
: struct with fields
input_unc: [1x1 ultidyn] sensor_gain: [1x1 ureal] unc_pole: [1x1 ureal]
pathinfo(:,1) % paths to USS blocks
= ans
3x1 cell array
{'usim_model/Plant' } {'usim_model/Sensor Gain' } {'usim_model/Unmodeled Plant Dynamics'}
سپس از usample برای تولید مقادیر عدم قطعیت uval متناسب با دامنههای عدم قطعیت مشخص شده استفاده کنید. به عنوان مثال، میتوانید پاسخ حلقه بسته را برای ۱۰ مقدار تصادفی از unc_pole، input_unc و sensor_gain به صورت زیر شبیهسازی کنید:
for i=1:10; uval = usample(uvars); % generate random instance of uncertain variables
sim('usim_model',10); % simulate response
end
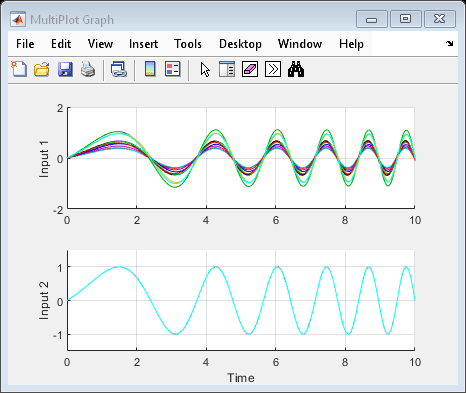
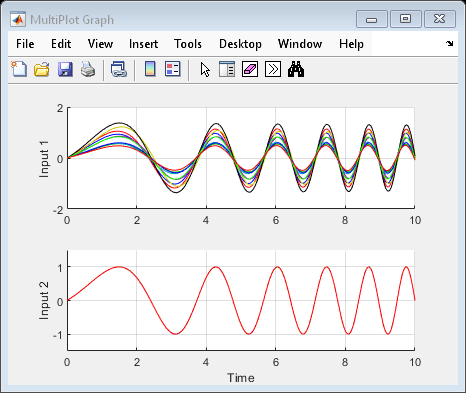
پنجره نمودار MultiPlot اکنون ۱۰ پاسخ ممکن از حلقه بازخورد نامشخص را نشان میدهد. توجه داشته باشید که هر نمونه uval یک ساختار است که شامل مقادیر متغیرهای نامشخص input_unc، sensor_gain و unc_pole میباشد:
uval % sample value of uncertain variables
= uval
struct with fields:
input_unc: [1x1 ss] sensor_gain: 0.5893 unc_pole: -4.9557
شبیه سازی های تصادفی
در صورت نیاز، میتوانید مدل را طوری پیکربندی کنید که برای هر شبیهسازی جدید از مقدار عدم قطعیت متفاوتی به نام uval استفاده کند. برای این کار، uvars را به فضای کاری Base یا Model اضافه کنید و فراخوانی usample را به تابع InitFcn مدل متصل کنید:
bdclose('usim_model'), open_system('usim_model')
% Write the uncertain variable list in the Base Workspace
evalin('base','uvars=ufind(''usim_model'');')
% Modify the model InitFcn
set_param('usim_model','InitFcn','uval = usample(uvars);');
% Simulate ten times (same as pressing "Start simulation" ten times)
for i=1:10; sim('usim_model',10);
end
% Clean up
set_param('usim_model','InitFcn','');
خطیسازی مدلهای نامشخص سیمولینک
اگر شما از سیمولینک کنترل دیزاین™ استفاده میکنید، میتوانید از همان روند برای خطیسازی و تحلیل سیستمهای نامشخص در حوزه فرکانس استفاده کنید. به عنوان مثال، میتوانید پاسخ بُده حلقه بسته را برای ۱۰ نمونه تصادفی از عدم قطعیت مدل ترسیم کنید:
clear sys
wmax = 50; % max natural frequency for unmodeled dynamics (input_unc)
for i=1:10; uval = usample(uvars,1,wmax); sys(:,:,i) = linearize('usim_model');
end
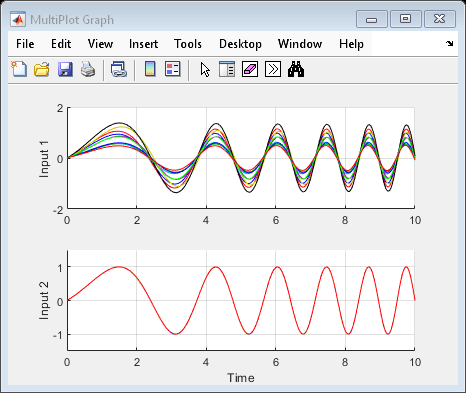
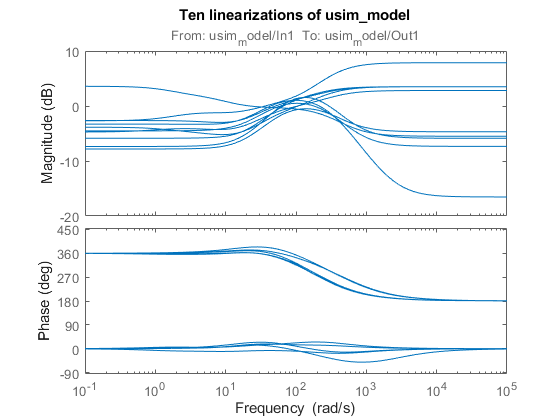
bode(sys) title('Ten linearizations of usim\_model');
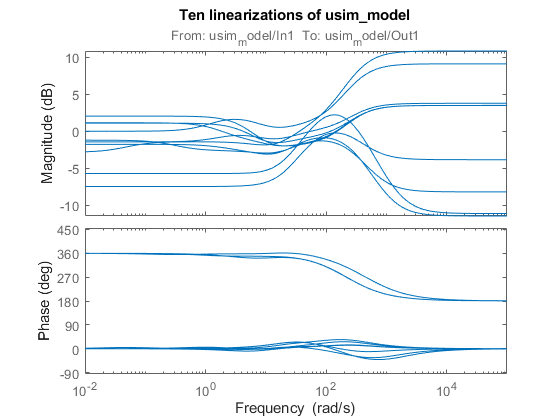
اگر نقطه عملیاتی مستقل از متغیرهای نامشخص باشد، یک روش سریعتر این است که یک خطیسازی نامشخص (شیء USS) را بهصورت یکجا با استفاده از دستور ulinearize محاسبه کنیم:
usys = ulinearize('usim_model')
Uncertain continuous-time state-space model with 1 outputs, 1 inputs, 3 states. The model uncertainty consists of the following blocks: input_unc: Uncertain 1x1 LTI, peak gain = 1, 1 occurrences sensor_gain: Uncertain real, nominal = 1, range = [0.1,2], 1 occurrences unc_pole: Uncertain real, nominal = -5, range = [-10,-4], 1 occurrences
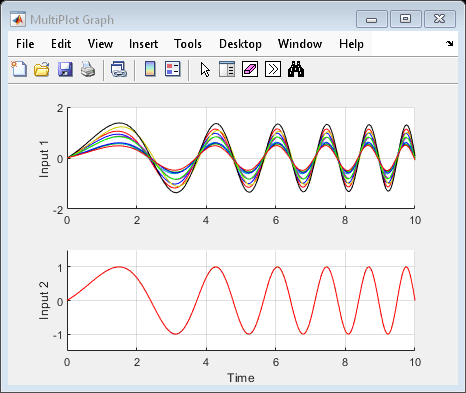
سپس میتوانید مدل فضای حالت نامشخص usys را نمونهبرداری کنید تا یک نمودار بود مشابه تولید کنید:
bode(usample(usys,10,wmax)) title('Ten linearizations of usim\_model');

 09112441370
09112441370

دیدگاه خود را بنویسید